Author: Gouri Nangliya
Neural Networks find extensive applications in areas where traditional computers don’t fare too well. Today, neural networks are used for solving many business problems such as sales forecasting, customer research, data validation, and risk management. So, can you fool neural network? Sounds fun, right! This blog explains one of the techniques to fool neural network into doing something it was not intended to do. Basically, this blog is a summary of paper titled ADVERSARIAL REPROGRAMMING OF NEURAL NETWORKS.
INTRODUCTION
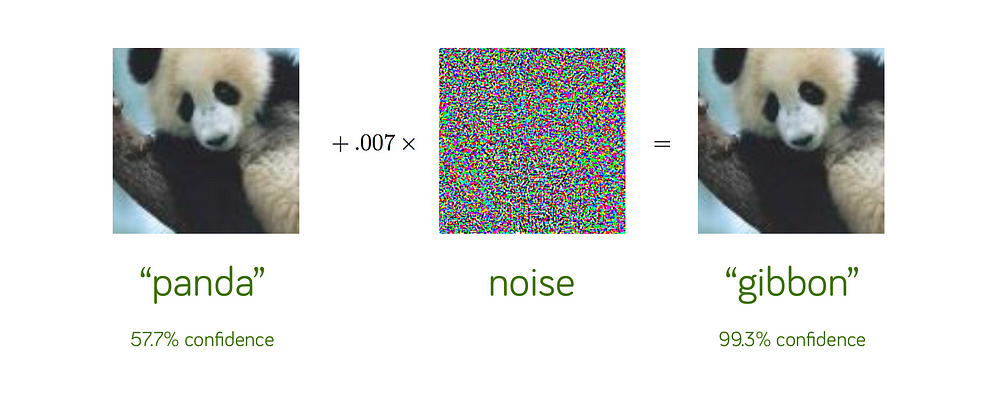
Well, it seems deep neural networks are susceptible to adversarial attacks. An adversarial attack consists of subtly modifying an original image in such a way that the changes are almost undetectable to the human eye. The modified image is called an adversarial image, and when submitted to a classifier is misclassified, while the original one is correctly classified. Adversarial examples are such inputs to model that attacker has intentionally created so that model can make mistake. This is done by taking an image from dataset and using gradient descent to search for a nearby image on which model makes mistake. To make things more clear, look at example below : a model classifies image as “panda” with 57.7% confidence(image on left). But, when little carefully crafted noise is added, same model classifies new image as “gibbon” with 99.3% confidence(image on right). Now, you can clearly see, we can’t differentiate between image on left and image on right. But, this tricks the model!
One such concept is Adversarial Reprogramming of neural networks - in which model performs a task choosen by attacker which it was not intended to perform. Attacker just add slight change in all test inputs and reprogram the model to perform the new task. Attacks can be either a model is targeted to classify as a single output for all(or majority) of inputs or just degrade the performance of the network by misclassifying the inputs.
Consider a model trained to perform some original task: for inputs $x$, it produces output $f(x)$. Consider an adversary(attacker) who wishes to perform an adversarial task: for inputs $x’$ (not in domain of $x$), it wishes to produce an output $g(x’)$. So, this task can be done by using adversarial reprogramming functions, $h_f(.;\theta)$ and $h_g(.;\theta)$ where $h_f$ converts input from $x’$ into domain of $x$ and $h_g$ converts outputs i.e $f(h (.;\theta))$ to $g(x’)$. Now, we compute $\theta$ to get the equation: $h_g(f (h_f (x’))$ = $g(x’)$. Here, $\theta$ is known as adversarial reprogram.
In this blog, we will look at adversarial reprogramming for MNIST classification. So, the idea is, we embedded MNIST digits of size 28 × 28 × 3 inside the original CIFAR-10 image, assign the first 10 CIFAR-10 labels to the MNIST digits, and train an adversarial program. So, in this case, $x$ will be CIFAR-10 images and $x’$ will be MNIST images, $f(x)$ will be classifying CIFAR-10 images into one of the 10 labels and $g(x)$ as you can guess will be classifying MNIST images into 0-9 i.e. again 10 labels. Results show that it can be successfully reprogrammed to function as an MNIST classifier.
Diving into Maths behind this!
Adversarial reprogram is something added to input. Consider ImageNet classifer for CIFAR10. Adversarial reprogram is defined as : $P = \tanh( W \odot M )$ where $W \in \mathbb{R}^{nxnx3}$ is the parameter to be learned n is CIFAR10 image width M is masking matrix in which 0 - adversarial data for new task, 1 - otherwise. $\tanh(\odot)$ is needed to make perbutations in (-1,1) i.e the same range of images in which model is trained to classify.
The adversarial image(new input) becomes : $X_{adv} = h_f(x’;W) = X’ + P$ where $x’ \in \mathbb{R}^{nxnx3}$ is sample of MNIST dataset $X’ \in \mathbb{R}^{nxnx3}$ is equivalent CIFAR10 image which is obtained by placing $x’$ at the centre.
Let, $P(y|X)$ be the probability that it predicted $y$ for the given input image $X$ where $y \in {1,…,1000}$. Now, we define $h_g(y_{adv})$ be the hard-coded mapping function that maps $y_{adv}$ to set of ImageNet labels. So, our goal is to maximize $P(h_g(y_{adv})|X_{adv})$. Theresore, optimization problem can be seen as : $W’ = \underset{W}{argmin}(-logP(h_g(y_{adv})|X_{adv}) + \lambda||W||^2_F)$ where $\lambda$ is regularization coefficient to reduce overfitting. So, attacker only need to add this data and store the program, majority of computation will be done by targeted network.
How to build MNIST classifier?
Follow steps below:
- Take a pretrained model on ImageNet like ResNet. If you are using CIFAR-10 dataset, then don’t use pretrained, weights don’t transfer well.
- Add last fully connected layer for 10 output classes(0-9).
- Train the model on CIFAR-10.
- Add an adversarial program image to your MNIST image and pass that through the model. Map the outputs of model using the remapping you chose above to get your MNIST predictions.
- Train only the adversarial program image on the remapped labels, while keeping the ResNet weights frozen.
Now you got yourself an MNIST classifier: Take an MNIST image, add on your trained adversarial program, run it through ResNet, and remap its labels to get predictions for MNIST.

Experiments
The key point in bulding this MNIST is that we need to optimize in image space so that classification loss decreases. Actual size of CIFAR10 is 32x32 and that of MNIST image is 28x28. After implementing this MNIST classifier, I tried different sizes for MNIST images which is to be placed at the center of CIFAR10 images. Take a look at adversarial examples below for 14x14 MNIST images. As you can see, the MNIST image of size 14x14 placed at center of 32x32 image and rest of image space has some well crafted noise which helps us to build MNIST classifier.

Below are the accuracy plots for learning rates 0.01 and 0.1 respectively.


So, we can see from the figure that as size of MNIST image is decreasing, accuracy is increasing. This is because the area in which model needs to optimize i.e. (32x32 - adversarial image area) is increasing and so is the accuracy. The drop of accuarcy at size 7x7 is due the fact that for odd number, my implementation doesn’t place adversarial image at center. So, this reveals another property that by placing the adversarial image at center, we get more accuracy than placing at any other location.
So, this is how you can fool a neural network. Adversarial examples make machine learning models vulnerable to attacks, as in the following scenarios. A self-driving car crashes into another car because it ignores a stop sign. Someone had placed a picture over the sign, which looks like a stop sign with a little dirt for humans, but was designed to look like a parking prohibition sign for the sign recognition software of the car. A spam detector fails to classify an email as spam. The spam mail has been designed to resemble a normal email, but with the intention of cheating the recipient. A machine-learning powered scanner scans suitcases for weapons at the airport. A knife was developed to avoid detection by making the system think it is an umbrella.
References :
- Adversarial Reprogramming of Neural Networks - https://arxiv.org/pdf/1806.11146.pdf
- https://medium.com/@ml.at.berkeley/tricking-neural-networks-create-your-own-adversarial-examples-a61eb7620fd8
- https://towardsdatascience.com/adversarial-examples-in-deep-learning-be0b08a94953
- https://rajatvd.github.io/Exploring-Adversarial-Reprogramming/
- https://medium.com/onfido-tech/adversarial-attacks-and-defences-for-convolutional-neural-networks-66915ece52e7